복소수 이제는 기억도 잘 나지 않는데, 전기기사 회로이론에 등장해서 매우 곤란했지만 다행히 잘 짚고 넘어갈 수 있었습니다.
생각보다 복잡하게 사용되지 않았으며 어떻게 표현될 수 있으며 곱셈, 덧셈하는 방법 그리고 변환하는 것까지만 잘 이해하려고 노력했습니다.
전기기사 취득을 위해서 머리띠를 꽉 동여맨 만큼 지금 이 글을 보고 있는 여러분들도 같이 좋은 결과 얻었으면 좋겠습니다.
복소수 활용
교류 회로를 해석하는데 순시값으로 표현되는 정현파를 간단하게 복소수의 계산으로 해결 가능하다고 합니다.
총 4가지 형식(직각좌표, 극좌표, 삼각함수, 지수함수)으로 표현함으로써 회로 계산을 편리하게 할 수 있도록 도와준다고 해요.
저도 이제는 기억이 가물가물해서 '어떻게 해야지'하고 우려가 조금 섞여 접근했지만 알고보면 모르는 사람도 충분히 이해하고 적용할 수 있더라고요.
실제 복소수가 어떤 형태인지 암기만 잘 해도 된다고 하니, 제가 알고 있는 요점과 암기 사항을 아래와 같이 정리해볼께요.
1. 복소수(complex number)
복소수는 말 그대로 두 개의 요소로 이루어진 수라는 뜻으로 전기에서는 𝒂 + 𝒋𝒃 형태로 표현합니다.
- 𝒂 = 실수부(real part)
- 𝒃 = 허수부(imaginary part)
위와 같은 복소수를 좌표에 표시할 때에는 복소평면(가로는 실수축, 세로는 허수축)에 그려볼 수 있습니다.
그렇다면 가로는 실수축이기 때문에 '1'이라고 표현할 수 있으며 허수축은 'j'라고 표현할 수 있겠죠.
- 실수: 제곱하면 양이 되는 수
- 허수: 제곱하면 음이 되는 수
그렇다면 𝒂 + 𝒋𝒃를 복소평면에 그려보면 아래와 같이 실수측(𝒙)에는 'a = 1'이 허수측(𝒚)에는 'jb = j'가 그려질 수 있습니다.
그러면 그래프로 봤을때 실수 '1'과 허수 '𝒋'의 각도가 다른 것을 알 수 있습니다. 교류 파형에서 반시계 방향이 양의 각이라고 알려준 걸 대입하면,
실수측 1에서 90도(x)를 곱하면 '𝒋'가 되고, '𝒋'에 또 90도(x) 곱하면 '-1'이 되는 걸 알 수 있습니다.
그럼 여기서 x값을 허수인 '𝒋'로 표현하면 '𝒋'는 √-1 이 되는 걸 알 수 있습니다.
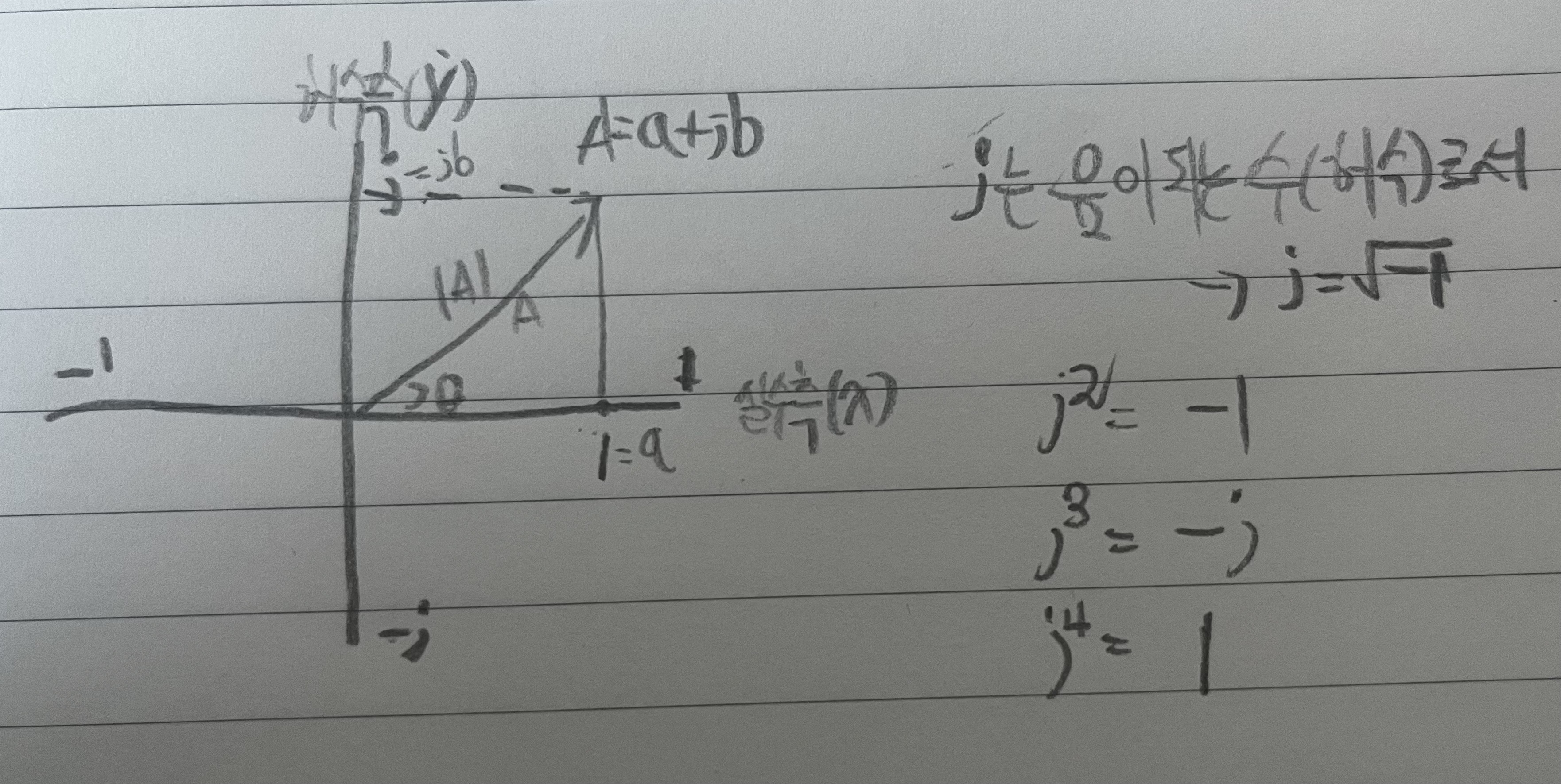
정리하자면 아래와 같이 외우면 되겠습니다.
𝒋 = √-1, 𝒋² = -1, 𝒋³ = -j
결론은 위와 같이 '𝒋'를 통해 현재 그래프상에 어떤 위상을 가지고 있는지도 알아볼 수 있습니다.
𝒋 = √-1 = 1∠90º = 1∠-270º
𝒋² = -1 = 1∠180º
𝒋³ = -j = 1∠270º
2. 복소수의 표현
이제 어느정도 회로이론에서 쓰이는 𝒋의 느낌을 알았다면 이걸 4가지 방법으로 표현하고 어떻게 전환하는지 알아야하는데요.
사실 한가지 방법만 알면 계산기로 쉽게 구할 수 있답니다.
저희가 위에서 사용한 '𝒂 + 𝒋𝒃' 형태는 직각좌표 형식으로 표현했다고 생각하시면 됩니다. 이를 극좌표, 삼각함수, 지수함수로도 표현할 수 있어요.
1) 직각좌표 형식
𝑨 = √a² + b²
- 복소수 𝑨의 크기는 피타고라스 정리 = √a² + b²
- 위상의 크기는 𝜽 = ± tan-1 b/a
- 예를 들어 𝑨 = 3 + 𝒋4라면
- 크기 '𝑨'는 피타고라스 정리에 따라서√3²+4² = 5
- 위상 𝜽 = tan-1 4/3 = 53.13º
- 즉 크기는 5, 위상은 53.13º가 나옴을 알 수 있죠
2) 극좌표 형식
위와 같이 직각좌표에서 계산한 크기와 위상을 극좌표로 간단하게 아래와 같이 표현할 수 있습니다.
- 𝑨 = 𝒂±𝒋𝒃 = 𝑨∠±𝜽
- 5∠53.13º(극좌표 형식 표현)
3) 심각함수 형식
삼각함수 형식 같은 경우 직각좌표에서 Cos𝜽값과, sin𝜽로 크기 '𝑨'를 구할 수 있는 걸 뜻합니다.
- 𝑨 = 𝒂±𝒋𝒃 = 𝑨∠±𝜽 = 𝑨(cos𝜽 ± 𝒋sin𝜽)
- 5(cos53.13º + 𝒋sin53.13º)
4) 지수함수 표현
지수함수는 크기 𝑨, 지수 𝒆, 위상𝜽 표현 함을 뜻합니다.
- 𝑨 = 𝒂±𝒋𝒃 = 𝑨∠±𝜽 = 𝑨(cos𝜽 ± 𝒋sin𝜽) = 𝑨𝒆제곱 형식으로 ±𝒋𝜽
- 5𝒆제곱 형식𝒋53.13º
이제 전기기사 회로이론 시험문제를 살펴보면 직각좌표를 극좌표, 극좌표를 직각좌표 등 변환해서 어떻게 표현해야 하는지 알아야 하는데요.
간편하게 직각좌표 같은 경우 극좌표로 변환할 수 있지만, 극좌표를 직각좌표로 변환하기 위해서는 삼각함수 형식을 이용해서 전환할 수 있습니다.
2. 복소수의 덧셈, 뺄샘, 곱셈, 나눗셈
그렇다면 복소수 산수는 어떻게 하면 될까요? 저도 아주 어렵게 생각하고 복잡하겠지하고 봤지만 생각보다 어렵지 않게 해결할 수 있습니다.
1) 덧셈과 뺄셈
- 덧셈과 뺄셈은 아주 쉽게 할 수 있습니다. 2개의 복소수가 주어지고 덧셈, 뺄셈을 하라고 할 경우
- 실수는 실수끼리, 허수는 허수끼리 연산해주면 됩니다.
- 매우 쉽게 하실 수 있습니다. 있는 그대로 더하거나 빼주면 끝!
- 반드시 실수끼리, 허수는 허수끼리
2) 곱셈과 나눗셈
- 곱셈과 나눗셈을 편하게 하려면 극좌표 형식으로 변환하여 하는 걸 추천
- 곱셈은 크기는 크기끼리 곱하고, 위상은 위상끼리 더하기(극좌표 형식에서)
- 나눗셈은 크기는 크기끼리 나누고, 위상은 위상끼리 빼준다(극좌표 형식)
이렇게 극좌표로 변환해서 곱셈과 나눗셈을 한 뒤에 다시 삼각함수 변환을 통해 직각좌표 형식으로 값이 얼마인지 알 수 있습니다.
총정리
복소수는 교류의 순시값을 편리하게 알기 위해서 쓰일 수 있으며 복소평면에 그려 표현할 수 있습니다.
실수측과 허수측으로 구분하여 식으로 표현하며 총 4가지 형식으로 나타낼 수 있으며 이에 따라 연산도 용이하게 할 수 있어요.
허수 𝒋의 표현과 4가지 형식의 변환 그리고 연산 방법까지 알아두시면 좋을 것 같습니다.
저도 아직 이론만 계속 공부하고 있는데, 기출문제를 풀어보는 것도 매우 중요하다고 해요. 꾸준하게 화이팅 합시다.
'제주라이프 > 라이프스타일' 카테고리의 다른 글
| R-L-C 직렬 회로 알려드립니다.(직렬 공진, 전압확대비) (1) | 2024.11.20 |
|---|---|
| 교류회로의 저항 인덕턴스 커패시턴스(R, L, C) (0) | 2024.11.18 |
| 정현파 교류의 표현: 순시값, 평균값, 실효값 등! (0) | 2024.11.16 |
| 전기기사 회로이론 교류 파형 기초(주파수와 주기, 도수법과 호도법 등) (0) | 2024.11.15 |
| 청년도약계좌 기여금 신청방법 알려드립니다.(2025년 기준) (0) | 2024.11.14 |



